MATRICES (TRAITEMENT NUMÉRIQUE DES)

MATRICES (TRAITEMENT NUMÉRIQUE DES)

Nous désignons par A une matrice à n lignes et p colonnes. L’élément de la i -ième ligne et de la j -ième colonne de A est un nombre complexe noté a ^{i , j} .

Les problèmes de calcul numérique les plus courants liés aux matrices sont la résolution de systèmes linéaires, l’inversion de matrices carrées et le calcul des valeurs propres et des vecteurs propres d’une matrice.

L’importance de ces problèmes provient du fait que les opérateurs linéaires sont les plus simples, donc les mieux connus. Ainsi ils constituent pour la mathématique appliquée un modèle agréable pour traiter un problème. De plus, on est souvent conduit à approcher la solution d’un problème non linéaire par des opérateurs linéaires: un exemple typique est l’utilisation de la méthode de Newton pour résoudre un système d’équations non linéaires, qui conduit à résoudre à chaque pas un système linéaire.

Les systèmes linéaires interviennent lors de la résolution numérique d’équations différentielles ou d’équations aux dérivées partielles, de problèmes d’approximation ou d’interpolation.

Les problèmes de valeurs propres proviennent de l’étude des vibrations, de la stabilité ou de la résonance des systèmes physiques linéaires, ou encore de l’analyse factorielle.

Précisons que les calculs sont faits, toujours, pour des matrices d’ordre élevé (entre 10 000 et 100 000 par exemple); l’outil utilisé est un ordinateur. De plus, nous examinons ici, parmi les méthodes possibles, celles qui paraissent le mieux adaptées au calcul numérique, donc les plus utilisées.

Dans beaucoup de méthodes, il est fondamental de remplacer la matrice considérée par une matrice de forme plus simple.

1. Factorisation des matrices

Soit A une matrice carrée (n = p ) inversible; alors, il existe une matrice de permutation P telle que la matrice P A puisse se factoriser en un produit d’une matrice L triangulaire inférieure à diagonale unité et d’une matrice R triangulaire supérieure. Pour P fixé convenable cette factorisation est unique.

Parmi les méthodes numériques, citons la méthode de Gauss et celle de Cholesky.

Méthode de Gauss

La méthode de Gauss est la méthode classique d’élimination. Elle consiste à engendrer une suite de n matrices A ^(r) , où r = 1, 2, ..., n , de la forme:

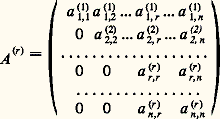avec det A ^(r) 0.

On part de A = A ⁽¹⁾ et on passe de la matrice A ^(r) à la matrice A ^(r+1) de la façon suivante. Puisque det A ^(r) 0, et quitte à faire une permutation des n 漣 r + 1 dernières lignes , on peut supposer a ^{(r) r ,r} non nul (cela revient à remplacer A ^(r) par une matrice de la forme P ^(r) 練 A ^(r) , où P ^(r) est une matrice de permutation).

On pose:

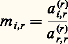dans laquelle tous les termes sont nuls à l’exception de ceux de la diagonale (qui sont égaux à 1) et de ceux de la r -ième colonne situés au-dessous de la diagonale.

On définit maintenant:

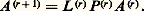La matrice A ⁽ⁿ⁾ est triangulaire supérieure. On vérifie alors que:

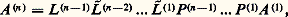où 籠 ^(r) se déduit de L ^(r) en permutant un certain nombre d’éléments 漣 m ⁱ ,^r . On a donc:

si l’on pose:

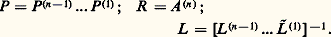Les coefficients a ^{(r) r} ,^r , appelés pivots, jouent dans la mise en œuvre de la méthode un rôle décisif. Dans la méthode décrite ci-dessus, on peut choisir le pivot dans la colonne r parmi les n 漣 r + 1 lignes restantes. Or il est clair que, pour des raisons de stabilité (on divise par a ^{(r) r ,r} ), on a intérêt à choisir |a ^{(r) r ,r} | le plus grand possible; c’est ce qu’on fait dans la pratique. La méthode précédente, avec cette stratégie de pivot, s’appelle méthode de Gauss par pivot partiel .

Une variante consiste à choisir comme pivot l’élément de plus grand module de la matrice carrée d’ordre n 漣 r + 1 restant à transformer au r -ième pas; cela revient à trouver deux matrices de permutation P et S telles que:

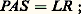c’est la méthode de Gauss par pivot total .

Ces deux manières de choisir les pivots conduisent à des algorithmes stables; on ne peut cependant pas garantir en général la stabilité de la méthode de Gauss utilisée sans une stratégie de pivot convenable.

Pour une matrice A d’ordre n , la méthode de Gauss utilise un nombre d’opérations élémentaires de l’ordre de 2 n ³/3.

Méthode de Cholesky

La méthode de Cholesky s’applique au cas de matrices réelles symétriques définies positives. La factorisation obtenue est de la forme A = LL , où L est la transposée de L et où L est une matrice à éléments diagonaux positifs.

Un autre type de décomposition consiste à écrire la matrice A sous la forme du produit QR d’une matrice unitaire Q par une matrice triangulaire supérieure R . Une telle factorisation est toujours possible (méthodes de Householder et de Givens).

2. Résolution des systèmes linéaires

A est une matrice carrée inversible d’ordre n à éléments réels; on cherche x , vecteur colonne de Rⁿ vérifiant:

où b est donné dans Rⁿ ; ce qui équivaut au système:

où i = 1, 2, ..., n .

Si on remplace R par C, on peut toujours se ramener à la situation précédente. Nous distinguerons deux types d’algorithmes, les algorithmes directs et les algorithmes itératifs.

Méthodes directes

Les méthodes directes sont particulièrement adaptées aux systèmes linéaires pleins (c’est-à-dire ceux dont la matrice contient peu d’éléments non nuls) et d’ordre «peu élevé». En fait, dans l’état actuel de la technique, un ordinateur permet de résoudre par ces méthodes, et de façon précise et économique, des systèmes linéaires pleins d’ordre supérieur à 400.

On appelle méthode directe de résolution d’un système linéaire une méthode qui permet d’obtenir la solution de ce système en effectuant un nombre fini d’opérations élémentaires (addition, multiplication, division, extraction de racine carrée) sur des nombres réels. Le coût (au sens économique du terme) peut être convenablement représenté par le nombre des opérations élémentaires qu’elle nécessite. Puisque chaque opération élémentaire est généralement entachée d’une erreur d’arrondi, la solution calculée diffère toujours de la solution exacte, et parfois elle peut n’avoir qu’un lointain rapport avec cette dernière. On est donc conduit à introduire la notion de stabilité d’une méthode directe; de façon grossière, on dira qu’une telle méthode est stable si elle est peu sensible à l’accumulation des erreurs d’arrondi. De plus, cette notion dépend de la matrice à laquelle on applique la méthode. On montre que, si 瑩A 瑩 est une norme de la matrice A (inversible), le nombre 瑩A 瑩 練 瑩A ^-1 瑩, appelé nombre de condition de la matrice A , permet de mesurer la stabilité de la méthode, qui est d’autant plus mauvaise que ce nombre est plus grand (quand ce nombre est grand, on dit que la matrice est mal conditionnée).

Les méthodes que nous donnerons seront donc les moins coûteuses et seront toujours stables.

On utilise les factorisations obtenues au chapitre 1: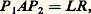

où P ¹ et P ² sont matrices de permutation, ou bien:

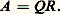Alors, le système () s’écrit:

qui équivaut à Ux = y et Ly = b , ou:

qui équivaut à Rx = Q ^-1b = Q b = b ; notons que Q ^-1 s’obtient sans calcul, donc sans erreur, comme la matrice Q , transposée de Q , puisque Q est unitaire.

On se ramène donc à la résolution de un ou deux systèmes à matrice triangulaire, ce qui est immédiat par n ² opérations élémentaires. Le point crucial dans les méthodes directes est donc celui des factorisations.

Il est clair enfin que l’inversion d’une matrice carrée d’ordre n équivaut à la résolution de n systèmes linéaires et que les factorisations LR et QR permettent le calcul du déterminant de A .

Méthodes itératives

Les méthodes itératives sont adaptées aux grands systèmes linéaires à matrices bande (c’est-à-dire que a ^{i ,j} = 0 pour |i 漣 j | 礪 m et que m est petit devant n ). On construit une suite (x ^(p) ) d’éléments de Rⁿ qui converge vers x , solution de () lorsque p tend vers l’infini, le calcul de x ^(p) devant être (si possible) nettement plus simple que la résolution du système considéré.

On écrit l’équation () sous la forme:

où A = M 漣 N et où M est inversible.

On choisit x ⁽⁰⁾ quelconque et on définit x ^(p+1) à partir de x ^(p) par:

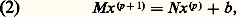soit:

Les problèmes sont alors les suivants:

a ) convergence de la suite (x ^(p) ); remarquons que si elle converge c’est nécessairement vers x ;

b ) choix de M pour que M soit facilement inversible et que la suite (x ^(p) ) soit «rapidement» convergente.

Pour la convergence, si l’on pose M ^-1N = B , il résulte de (1) et de (2) que:

donc la suite (x ^(p) ) est convergente pour tout choix de x ⁽⁰⁾, si et seulement si:

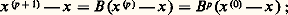
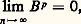ce qui équivaut à:

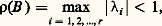les nombres¹,², ...,^r étant les valeurs propres de B .

Pour comparer plusieurs méthodes, on montre que la convergence est d’autant plus rapide que le nombre 漣 ln 福(B ), appelé ordre de convergence asymptotique de B , est plus grand.

Pour le choix de M , voici quelques exemples.

On définit à l’aide de la matrice A les matrices:

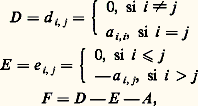et l’on suppose D non singulière: a ⁱ ,ⁱ 0 pour i = 1, 2, ..., n . On peut prendre les décompositions suivantes de A = M 漣 N .

a ) Méthode de Jacobi :

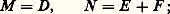b ) Méthode de Gauss-Seidel :

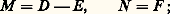c ) Méthode des relaxations successives : soit 諸 un nombre réel non nul appelé paramètre de relaxation:

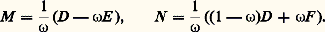D’autres méthodes plus élaborées sont d’un usage intéressant pour certains types de problèmes, comme la méthode des directions alternées, et la méthode des pas fractionnaires où l’on construit x ^(p+1) à partir de x ^(p) en plusieurs temps.

Signalons enfin les méthodes de gradient (ou de descente), fondées sur la remarque suivante: si A est une matrice symétrique réelle, définie positive, la solution du système () est l’unique élément de Rⁿ qui minimise la forme quadratique définie par:

où (, ) désigne le produit scalaire dans Rⁿ .

Naturellement, dans la mise en œuvre sur ordinateur d’une méthode itérative, la solution calculée est x ^(p) pour p «assez grand»; il faut donc disposer d’un critère (test d’arrêt) pour arrêter le calcul à un rang p convenable.

3. Calcul des éléments propres d’une matrice

On s’intéresse d’abord à la recherche de toutes les valeurs propres.

Si une matrice A est symétrique, ses valeurs propresⁱ ont la propriété de stabilité suivante.

Soit B = A + E une matrice symétrique de valeurs propres 猪; alors on peut associer deux à deux les valeurs propresⁱ et 猪ⁱ de façon que:

où i = 1, 2, ..., r .

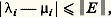Or l’analyse de l’erreur montre que le calcul numérique des valeurs propres de A se ramène au calcul des valeurs propres d’une matrice perturbée B = A + E symétrique.

Par contre, si les matrices considérées ne sont plus symétriques, le résultat devient:

où P est un polynôme et où i = 1, 2, ..., r .

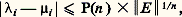Nous distinguerons maintenant ces deux cas.

Matrices symétriques

Pour les matrices symétriques, on peut utiliser plusieurs méthodes.

a ) La méthode de Jacobi consiste à construire une suite de matrices unitairement semblables à A :

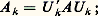A ^k converge vers une matrice diagonale D dont les éléments diagonaux sont les valeurs propres de A . On calcule A ^k+1 à partir de A ^k en utilisant une rotation dans l’espace à deux dimensions défini par les indices i et j , telle que a ^{i ,j (k+1)} = 0.

Pour k assez grand, A ^k est «presque diagonale», les colonnes de la matrice unitaire U ^k définissent des approximations des vecteurs propres de A .

b ) Les méthodes de Householder (1959) et de Givens (1954) déjà citées, convenablement adaptées, permettent de tridiagonaliser une matrice symétrique. On calcule alors les valeurs propres d’une telle matrice (donc de la matrice initiale) en utilisant des résultats de localisation (méthode de bissection). L’obtention des vecteurs propres par ce genre de méthodes présente des difficultés liées à l’instabilité.

Précisons que la méthode de Householder est deux fois plus rapide que la méthode de Givens, ce qui fait souvent préférer la première.

Matrices quelconques

Pour les matrices quelconques, c’est-à-dire non nécessairement symétriques, le procédé le plus utilisé est l’algorithme QR avec «shift» k ^s , proposé simultanément par Francis et par Kublanovskaja en 1961. On remplace d’abord la matrice A par une matrice semblable de type Hessenberg supérieur, c’est-à-dire telle que a ^{i ,j} = 0 pour i 閭 j 漣 1 (algorithmes de Householder et de Givens déjà cités).

On construit une suite de matrices A ^s par:

où Q ^s est matrice adjointe de Q ^s et où Q ^s est une matrice unitaire telle que la matrice:

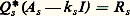soit triangulaire supérieure, c’est-à-dire que Q ^s R ^s représente une factorisation unitaire et triangulaire de la matrice A ^s 漣 k ^s I , où (k ^s ) est une suite de nombres complexes choisis convenablement; notons que la forme Hessenberg est conservée par toutes les matrices A ^s .

Cette méthode conduit toujours à une bonne approximation des valeurs propres. Le résultat le plus simple à formuler dans ce sens est le suivant: Si A a des valeurs propres¹,², ...,ⁿ vérifiant:

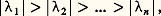la suite des matrices A ^s converge, lorsque s tend vers l’infini, vers une matrice triangulaire supérieure dont les éléments diagonaux sont les valeurs propres de A ; de plus, les valeurs propres sont rangées par modules décroissants. Pratiquement, une bonne approximation est obtenue en moins de dix itérations.

Signalons la méthode LR de Rutishauser (1958), fondée sur des idées analogues, mais utilisant une décomposition LR de la matrice A .

Ces méthodes s’appliquent avec succès au cas des matrices symétriques tridiagonales.

Le problème de la recherche des vecteurs propres reste difficile. La méthode semblant la plus satisfaisante est celle de l’itération inverse . On suppose connues les valeurs propres. Soit l’une d’elles. On choisit un vecteur x ⁽⁰⁾ de Rⁿ et on définit, pour k = 0, 1, 2, ..., le vecteur x ^(k+1) par:

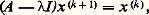ce qui revient à la résolution d’un système linéaire. Dans les bons cas, la suite (x ^(k) ) converge vers un vecteur propre associé à la valeur propre.

Quelques méthodes plus simples peuvent être utilisées lorsqu’on ne veut calculer que les valeurs propres dominantes, c’est-à-dire de plus grand module. Citons la méthode des puissances dont voici un exemple. Si A admet la valeur propre simple^M telle que |^M| 礪 |ⁱ | pour i M, si x ⁽⁰⁾ est un vecteur quelconque non orthogonal à la direction propre associée à^M, la suite définie par:

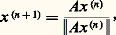où 瑩 瑩 désigne une norme dans Rⁿ , converge, lorsque n tend vers l’infini, vers le vecteur x tel que:

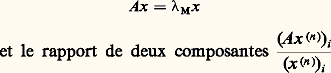tend vers^M.

Les méthodes numériques de l’algèbre linéaire sont satisfaisantes, à l’exception essentiellement du problème de la recherche des vecteurs propres. Les algorithmes sont donnés ici très brièvement, et ne sont utilisables que lorsqu’ils ont été traduits complètement dans un langage convenable (programmation), ce qui représente aussi beaucoup de difficultés techniques.

Signalons que quelques problèmes liés aux matrices n’ont pas été abordés ici, nous renvoyons en particulier aux articles OPTIMISATION ET CONTRÔLE et PROGRAMMATION MATHÉMATIQUE.

Encyclopédie Universelle. 2012.